Privacy Notice: I use a website analytics software. If you do not agree with its use, please leave this website.
This is the message for the visually-impaired or blind. This website is designed to be as screen-reader-friendly as possible to ensure that everyone is equally accessible to this content. Although the quality of the screen-reading varies from one screen reader software to another, this website is designed in a way that attempts to aid the screen-reader softwares to the greatest degree. I believe that everyone should be able to access education, regardless of your disability, because you matter as a student as much as any seeing students!
By Soup Isarangkoon
under the supervision of Dr. Eric Hill
6 Lab Classes
Have you ever touched a burning stove and it feels hot (if you are not having 3rd degree burn)? That is because heat is being ttransfered to your hands. In this site, we will define the thermal energy (heat) as \(Q\) or the part of the internal energy \(U\) that related to temperature.
Have you ever noticed how when you add the same amount of heat energy to different substance, the temperature changes very differently? For example, when you put a beaker of water and a block of aluminum of the same mass on the same stove set to the same temperature for the same amount of time, and you notice that water is barely just getting hot, while alumnium is getting red hot. That is because aluminum and water have a different specific heat (herein defined as \(c_V\)) From PHYS 233, we learned that this is an intrinsic characteristic of the substance that is specific and constant for that specific substance. We define specific heat as follows: $$\Delta Q=m\space c_V \Delta T$$ Although in most cases, this value \(c_V\) is constant, it actually is not, especially at low temperature as we will learn in this lab. If quantum-mechanical model is considered, specific heat is anything but a constant.
Using classical mechanics, one can model a sample of mass \(m\) made of \(N\) identical particles by modeling each atoms as point particles and bonds as massless springs. In this case, the internal energy \(U\) is made up of two components: Kinetic Energy \(T\) and Potential Energy \(V\).
Kinetic Energy of a single atom can be written as $$T=\frac 12 \frac mN \left(v_x^2+v_y^2+v_z^2\right)$$ Therefore, the total Kinetic Energy summed up from average \(T\) of each atom is
$$T_{net}=N\cdot \frac 12 \frac mN \left(v_x^2+v_y^2+v_z^2\right)$$
Using the formula for the motion of a molecule in one dimension deduced from the Boltzmann distribution, and finding rms of that, we found that the average kinetic energy in any one dimension is
\(\frac 12 k_B T\), therefore \(T_{net}\) becomes
$$T_{net}=3N\cdot \frac 12 k_BT$$
(note that it was multiplied by 3 because there are three dimensions total, and multiplied by \(N\) because there is \(N\) atoms total.)
Now, the potential energy of the bonds that are modeled as springs can be written as
$$V=\frac 12\left(k_x\Delta x^2+k_y\Delta y^2+k_z\Delta z^2\right)$$
Using a similar argument as earlier, one can say that average potential energy of the bond is \(\frac 12 k_B T\), therefore:
$$V_{net}=3N\cdot \frac 12 k_BT$$
As such \(U\), the total internal energy is
$$U=2\cdot \left(3N\cdot \frac 12 k_BT\right)=6N\cdot \frac 12 k_BT=3Nk_BT$$
If we say, there are an Avogrado's Number of atoms, therefore, there are one mole in the sample:
$$U\space (1\space mole)=3N_Ak_BT$$
Now \(N_Ak_B=R\) or the 'gas constant' and therefore:
$$U\space (1\space mole)=3RT$$
Using the first law of thermodynamics: \(\Delta U=\Delta Q-\Delta W\), where \(W\) is work, assuming that no work is done to the system, then \(\Delta U=\Delta Q\); as such, what was said earlier can be written as:
$$\Delta Q\space (1\space mole)=3R\Delta T$$
$$\frac{\Delta Q}{\Delta T}\space (1\space mole)=3R$$
Since \(\Delta Q=m\space c_V \Delta T\) and thus \(\frac{\Delta Q}{\Delta T}=m\space c_V\), therefore:
$$c_V\space (1\space mole)=3R$$
$$c_V\space (1\space mole)\approx 25 \space J/(mole\cdot K)$$
This means specific heat only depends on the molar mass of the substance and is always this exact value! Now, it would be no surprise to tell you that
this is wrong, and is not the case for certain substances like diamond, which has \(c_V\) value of \(6.2\space J/(mole\cdot K)\).
This is where quantum-mechanics and Einstein model comes in.
Instead of modeling as classical springs, what Einstein did was modeling the springs as a quantum simple harmonic oscillators.
From PHYS 233, we know that this energy level of the springs are quantized and that the energy level is equal to:
$$E_n=\left(n+\frac 12\right) \hbar \omega\qquad n=0,1,2,\dots$$
where \(\omega=\sqrt{k/m}\), in which, \(m\) is mass and \(k\) is the spring constant (NOT to be confused with Boltzmann constant \(k_B\) and \(n\) is the energy state index).
At temperature \(T\), on average, the oscillators are in the \(\bar{n}\)th excitation state as derived from the Bose-Einstein distribution as follows: $$\bar{n}(\omega,T)=\frac 1{e^{\hbar\omega/k_BT}-1}$$
Substituting \(\bar{n}\) into the equation for \(E_n\) gives the average oscillator energy as follows:
$$\bar{E}=\left(\frac 1{e^{\hbar\omega/k_BT}-1}+\frac 12\right)\hbar\omega$$
$$\bar{E}=\frac{\hbar\omega}{e^{\hbar\omega/k_BT}-1}+\frac {\hbar\omega}2$$
Since there are three oscillators per atom and an Avogrado's Number of atom in a mole of substance, we multiply \(\bar{E}\) by \(3N_A\) to get the internal energy \(U\) as follows:
$$U=3N_A\left(\frac{\hbar\omega}{e^{\hbar\omega/k_BT}-1}+\frac {\hbar\omega}2\right)$$
It is by definition that \(c_V=\frac{\Delta U}{\Delta T}\), therefore (assuming \(\Delta T\rightarrow 0\)):
$$c_V=\frac{d U}{d T}$$
$$c_V\space(1\space mole)=\frac{d}{d T}\left[3N_A\left(\frac{\hbar\omega}{e^{\hbar\omega/k_BT}-1}+\frac {\hbar\omega}2\right)\right]$$
$$c_V\space(1\space mole)=3N_A\cdot\frac{d}{d T}\left(\frac{\hbar\omega}{e^{\hbar\omega/k_BT}-1}\right)$$
$$c_V\space(1\space mole)=3N_A\cdot\hbar\omega\frac{d}{d T}\left({e^{\hbar\omega/k_BT}-1}\right)^{-1}$$
$$c_V\space(1\space mole)=-3N_A\cdot\frac{\hbar\omega}{\left(e^{\hbar\omega/k_BT}-1\right)^2} \frac{d}{dT}\left({e^{\hbar\omega/k_BT}-1}\right)$$
$$c_V\space(1\space mole)=3N_A\cdot\frac{\hbar^2\omega^2}{k_BT^2}\frac {e^{\hbar\omega/k_BT}}{\left(e^{\hbar\omega/k_BT}-1\right)^2}$$
$$c_V\space(1\space mole)=3N_Ak_B\left(\frac{\hbar\omega}{k_BT}\right)^2\frac {e^{\hbar\omega/k_BT}}{\left(e^{\hbar\omega/k_BT}-1\right)^2}$$
$$c_V\space(1\space mole)=3R\left(\frac{\hbar\omega}{k_BT}\right)^2\frac {e^{\hbar\omega/k_BT}}{\left(e^{\hbar\omega/k_BT}-1\right)^2}$$
Note that \(\hbar\omega/k_B\) is also called the Einstein's Temperature \(T_E\).
We see here that if \(k_BT>>\hbar\omega\), then \(c_V\space(1\space mole)\approx 3R\), matching the result of Dulong-Petit from earlier. This is however not true when the temperature is low and thus \(k_BT<<\hbar\omega\).
Firstly, start by following the cryogenic dewar setting-up instruction found here. Once you have finished following the instruction on that page, you will be
redirected back here. Now, add the three stainless-steel stud in the base plate,
as such, giving three support "towers" in the experimental space. Add a nut, two washers, and a thumb nut (in that order) into each stud.
Now, pass the three strings attached to the addendum, each in between the two washers on each stud, pull until all strings are taut and the
addendum is centered. Once that is done, screw in the thumbnut to hold the strings and the addendum in place.
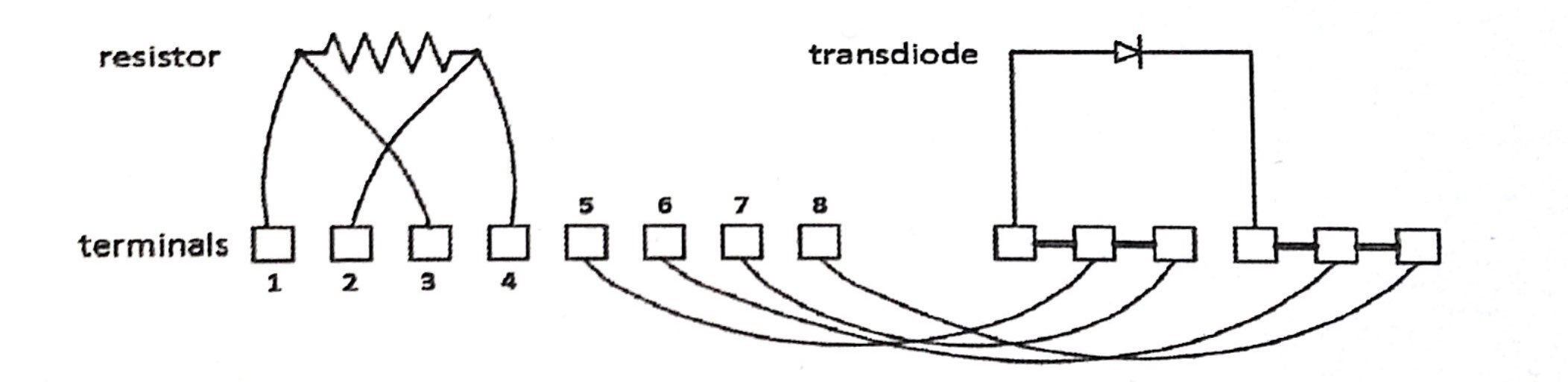
Underneath the addendum is a transdiode (which will act as a 'thermometer') and a resistor of 100 Ω resistance (which will act as a 'heater'). For the resistor, you will notice there are four leads. Choose one lead from each side of
the resistor and connect one of them to terminal 1, and another, to terminal 2 of the terminal strip. This will serve as leads where you pass in constant current through the resistor.
Take the two unused lead on the resistor and connect one to terminal 3, and another to terminal 4 of the terminal strip, so that terminal 1 and terminal 3 are linked, and terminal 2 and terminal 4 are linked. This will serve as voltage leads
where you will measure the voltage. For the transdiode, connect the terminal 5 and 7 together using a three-terminal connections on the extra green terrminal strip on the base plate. The permanent marker mark on the extra terminal green strip will indicate which terminals are connected.
Then, you will notice that for the connections you just made on the extra green terminal strip, there is one connection left. Connect the one lead of the transdiode to that connection.
Connect Terminal 6, 8, and the another lead of the transdiode using the same method as you did for Terminal 5 and 7.
In this case, terminal 5 and 7 will have a constant current passed through, and terminal 6 and 8 will be used to measure voltage as it changes with temperature — this will be used to measure the temperature.

STOP: Test (on the Cryostat Interface Box) the terminal 1/2, and terminal 3/4 pairs, there should be 100 Ω resistance! Pass \(10\mu A\) forward current through terminal 5/6 and terminal 7/8 pair, and measure a voltage drop — at room temperature, this should be 450 mV. If no current flows through, reverse the lead. Take note of which way the current flows.
Please pay attention to the set-up instructions at the beginning of Experiment 1 (below) as this set-up will need to be replicated in Experiment 2 and 3.
Choosing Sn (Tin) as your sample, place the sample onto the addendum. There are a few things one have to consider. Firstly, the brass addendum must remain flat and must make a contact with a flat face of the sample that are nearly mirror-smooth. Secondly, one must use the bare minimum quantity of vacuum grease to join the addendum and the sample together. You want a layer so thin that you cannot make any thinner either by squeezing the sample or sliding the sample around. Third, you will need three spring-steel clamps to hold thee sample securely to the addendum. This ensures that there is a good thermal contact at all times. The clamps are put on the sample by using the two steel clamp grabber.
Close up the dewar as shown on this page. Once done, you will be redirected back here. Then the next step is to set up the SIM900 Mainframe. This is an empty rack where you can insert many "SIMs" into it. The SIMs are tiny boxes that fits inside the SIM900 Mainframe. For this experiment, you will need the following SIM:
For the PI Temperature Controller SIM, you will notice that there are two banana jack ports (one positive and one negative), and a female RS-232 port on the back of the SIM. Connect a banana jack cable to the two banana jack ports (red for positive, black for negative), and connect a RS-232 cable into its corresponding port. Insert the PI Temperature Controller SIM into SIM900 rack, and pass the RS-232 cable and the banana plug cable through the back window of the SIM900 rack. Now connect the Set Pointt port in front of the SIM to a voltmeter (an adapter is needed). In front of this SIM, turn the big knob clockwise unti it no longer turns. Then adjust the gain to be \(4 \times 100\), and time constant to be \(10.6 \times 1\).
For Pulse Current SIM, connect a RS-232 cable into its corresponding port at the back of SIM, pass the cable through the back window of the SIM900 rack, and insert the Pulse Current SIM into the rack. For High-Gain Utility Amplifier SIM, simply insert the SIM into the rack without connecting anything.
For SIM922 Diode Temperature Monitor, connect two RS-232 cable to two RS-232 port at the back of the SIM. Take note of which cable is channel 1-2 and which is channel 3-4 on the back of SIM922.Pass the cable through the back window of the SIM900 rack, and insert the SIM922 into the rack.
Now, that all the SIMs are connected, you will need to wire up the Cryostat Interface Box. Connect the RS-232 cable from PI Temperature Controller SIM into the front-left RS-232 port on the Interface Box. Then connect the two RS-232 cables from SIM922 into the two right RS-232 ports (the cable connecting to channel 1-2 will be connected to the front-right port and the cable connecting to the channel 3-4 will be connected to the back-right port). Once complete, connect the remaining RS-232 cable from the Pulse Current SIM into the back-left RS-232 port on the Interface Box. Open the Cryostat Interface Box to start wiring. Once opened up, you will see that the wires leding from the front-left port are pre-connected with a zip tie that said "FIXED"; do not remove those as it was pre-wired by the instrument manufacturer. You will now have the Cryostat Interface that is connected as seen below in Figure 2 (I suggest you print out Figure 2 PDF here and annotate as you wire things up).
The next step is to wire the circuit that will send the current pulse to the resistor on the addendum to heat it up. To do this, connect Terminal 4 and 5 that leads to the Pulse Current SIM with Terminal 1 and 2 that leads to Addendum Terminal Strip inside the dewar. Now, connect Terminal 8 and 9 leading to Pulse Current SIM to Terminal 3 and 4 leading to the addendum terminal strip. This would allow the Pulse Current SIM to measure the voltage drop across the resistor, and output it in the "Voltage Monitor" BNC port in the front of the SIM. With this, the heating component of the addendum is now wired up.
The next step is to wire up the transdiode that allows us to measure the temperature of the addendum. Firstly, wire Terminal 1 and 2 that leads to the channel 1 and 2 of SIM922 to terminal 5 and 6 that leads to the addendum terminal strip. This would allow the SIM922 to supply a 10 μV current to the transdiode. Use Figure 2 to aid you in knowing which terminal should be connected with which as electricity only flows one way in a diode. Once this is done, connect Terminal 7 leading to the addendum terminal strip to BOTH Terminal 6 leading to channel 1-2 of SIM922 AND Terminal 1 of the BNC Connectors Strip. Then, connect Terminal 8 leading to the addendum terminal strip to BOTH Terminal 7 leading to channel 1-2 of SIM922 AND Terminal 3 of the BNC Connectors Strip. This allows the voltage drop across the transdiode to be simultaneously monitored through via BNC connectors, and via SIM922.
The next step is to wire the transdiode underneath the reservior to be able to measure the temperature of the reservior. To do this, connect Terminal 1 and 2 leading to the reservior, so that one terminal is connected to a V+ (2) and I+ (2) on the strip leading to channel 1-2 of SIM922, and the other terminal is connected to V-(2) and I-(2) on the strip leading to channel 1-2 of SIM922. Use Figure 2 to figure out which should go with which as the electricity only flows one way in a diode.
The next thing to do is to wire up the base plate, so that it also gives us the voltage drop (which allows us to convert into the temperature of the base plate). Although, this is already measured by and pre-wired-up to the PI Temperature Controller SIM, it is good if the output is also seen on SIM922. To do this, connect Terminal 6 and 7 leading to the base plate with Terminal 7 and 6 leading to channel 3-4 pf SIM922 (in that order), without removing what was previously wired.
To check that everything is working correctly, power up the SIM900 rack, without turning the DC power supplies on, and check that the following is true:
Power up an oscilloscope. Now connect a BNC cable between the Voltage Monitor port of the Pulse Current SIM, and Channel 2 of the oscilloscope. Connect BNC Port 1-2, and BNC Port 3-4 on the Cryostat Interface Box to Vin+ and Vin- port on the High-Gain Utility Amplifier (in that order). Then, connect the Output port of the High-Gain Utility Amplifier to the Channel 1 of the Oscilloscope.
Wait until the temperature of the addendum and base plate starts to stabilize — that is, the voltage drop of either the addendum or base plate fluctuates less than 0.2 mV per minute. Then close up the dewar as shown on this page. Please note that you will need to evacuate the both the space between the inner can and the outer can, as well as the space inside the inner can. Once done, you will be redirected back here.
Now, adjust the Pulse Current SIM, so that the time is set to 1 second, and current is set to 60 mA. Then on the High-Gain Utility Amplifier, set the first gain to 20 and second gain to 500, adjust the offset switch to be (-), and adjust the offset knob to 4.0 V (the inner digit is the decimal, the outer digit is tthe integer).
On the oscilloscope, turn CH1 and CH2 on, and adjust the VOLT/DIV knob of CH2, so that each box's width represent 1 V. Then, adjust the POSITION knob of CH2, so that the reading is in view. Then on CH1, adjust the VOLT/DIV knob to be 200 mV and adjust the POSITION knob to be between -500 mV and 500 mV (this way, it can be ensured that the reading is correct andd any flat line is not resulted from the reading hitting the maximum and minimum readable voltage at 15 and -15 V, respectively). Now, finely adjust the offset knob on the High-Gain Utility Amplifier SIM, so that the reading is in view. Lastly, adjust the HORIZONTAL SEC/DIV knob, so that M value is 25 seconds. Now, one is ready to begin the first experiment.
Please note that everything from the beginning of Experiment 1 to this point will be the same for Experiment 2 and 3, and these set-ups will need to be replicated for those experiments.
It is at this point, you know how the PI Temperature Controller SIM works. The SIM works by trying to heat up the baseplate and maintain the base plate temperature, in a way that the base plate transdiode voltage drop is exactly one tenth of what is set by the SIM's big knob, which is simultaneously outputted as the 'Set Point' voltage. The other thing you should know is that the base plate will 'couple' with the addendum and therefore, both will try to come to temperature equillibrum.
If the voltage of the CH1 of the oscilloscope is dropping, conversely, it means that the the addendum is cooling down as the coupled base plate is not hot enough. In this case, you will need to heat up the base plate slightly by adjusting the SIM's big knob, so the base plate is heated up. Do so until the graph on CH1 is slightly decreasing (the addendum is slightly warming up). If the voltage of the CH1 of the oscilloscope is steady, adjust the SIM's big knob, so the base plate is heated up. In either case, you will start seeing that the addendum voltage drop (seen in CH1 of the oscilloscope) will eventually be slightly decreasing — this is what is desired. Now that the voltage is dropping slightly, adjust the CH1 position knob on the oscilloscope, so the CH1 graph is at the top (but not out of) the screeen. Then, hit the RUN/STOP button twice, to clear the screen. Record the voltage drop of the addendum, then, press the toggle switch on the Pulse Current SIM to 'ON', and release the switch immediately. You will see that the current has been sent to the addendum to heat it up (seen on CH2 of the oscilloscope). You will see that the voltage drop of the addendum on the CH1 decrease and curve up slightly, before going down again. After that, waiit for a while for the CH1 curve to have a visibly steady slope (but do not wait until CH1 graph hits one square from the right edge of the screen, as it will start erasing your result), then click RUN/STOP once. You will now have a graph that looks like Figure 3.
Using a ruler and the oscilloscope's 'CH1 Amplitude' cursor function, mark that corresponds to when the current pulse was sent (shown in blue), and mark another point that corresponds to the location on the 'big drop' that directly intersects an imaginary line (blue dashed line) drawn tangentally to the steady-slope point (shown in red). The oscilloscope should show \(\Delta V\) or the voltage difference between the two points. Record this \(\Delta V\) along with its upper- and lower-bound uncertainty in your measurements, since using a ruler, you cannot be sure where the red dot exactly lands. Then, using the 'CH2 Amplitude' cursor, measure the voltage of the current pulse by placing one cursor at the bottom of the pulse and one at the top of the pulse.
Once this is done, you are ready for the next measurement. You will record 10 of these measurements; for each of these measurement, increase the addendum temperature/voltage drop by 5 mV. To heat up the addendum, send in constant current by flipping the toggle switch on the Pulse Current SIM to 'CW,' until the desired temperature is reached. Adjust the base plate accordingly by about the same amount as to keep the base plate very slightly warmer than the addendum.
After 10 measurements are made, stop the vacuum and opening up the dewar by going to this page. Once everything on that page has been followed, you will be redirected back to this page. Once here again, remove the inner can and then remove the Tin sample, while leaving the clip, addendum, and vacuum grease as intact as possible. Put the inner can back on wait for everything to equillibrate back to room temperature, and close up the dewar again by going to this page. Once everything on that page has been followed, you will be redirecteback to this page. Repeat all the steps from the lowest 'Red Bar' on this page onward to collect ten different measurements at roughly the same temperature. After this, you will be able to do data analysis.
You will be using Python in a Jupyter Notebook to process the data. You will be writing the Python code to process the data yourself. There are many approaches to code this Python program, so there is no one right answer here. That being said, this page will guide you through how the mathematical calculation to get the final data is done.
To process the data, the following steps need to be followed:
| V Reading (in mV) | T Reading (in K) |
|---|---|
| 425.8 | 296.25 |
| 738.4 | 194.7 |
| 994.4 | 77 |
inverse_function() function (without putting a parenthesis after a vectorized function). Then, pass in the upper-bound \(T\) value and lower-bound \(T\) value as the
second and third parameter to the inverse_function(). You will have to guess what the reasonable maximum and minimum value of your \(T\) (temperature) value should be.
If you don't know what to use, use 273.15 as the lower bound and 1000 as the upper bound, since the temperature you measure at this stage must be above the melting point of water
(273.15 K) but definitely less than 1000 K. This is a large range as it is only given as an example, therefore, if you use these numbers, even though you will get the right answer,
it will take a long time for the computer to process. So, choose you own reasonable upper and lower bound limit of your \(T\) (Temperature) value that you think the addendum might be experiencing.inverse_function() function, pass in a list or list-like object (like a numpy.array) that will contain the mV readings that you would
like to convert to K readings.
find_instantaneous_slopefunction; for the first parameter,
pass in the function you fit to the three points in Step 1 before it was vectorized without the parenthesis after it, then for the second parameter, pass in the temperature of the addendum when the \(\Delta V\)
was observed. The function will return the instaneous slope at that point or \(dV/dT\). You will now see that if you divide the actual \(\Delta V\) value from Step 2 to the \(dV/dT\) we just got, we will get \(\Delta T\) in K.
Once this is done, plot the graph of the \(c_V\) (specific heat) values for tin over the range of temperature you measured. The literature value of tin's specific heat is 0.213 J/g/K (at room temperature).
You will be using LN2 (Liquid Nitrogen) in this experiment. Be very careful. The person handling LN2 must wear protection mitts. Beware of it getting onto clothings, as it will get absorbed and cause instant frostibite. If spillage (especially on clothing) occurs, inform the instructor immediately!
In this experiment, you will be doing the same thing as in Experiment 1, except at cryogenic temperature.
Unlike in the last experiment, the instructions will not be as detailed as the last as you already have done this experiment once, so the instruction will
be brief, and will only outline what is different in this experiment only.
The initial set-up of this experiment is the same as the Experiment 1 to the extent indicated in the previous sections.
To do this, you will essentially repeat everything done in Experiment 1 with exception being that after the dewar is closed up
and both the chambers have been vacuum out, you need to pour in LN2 using a funnel to fill the reservior completely — that is until the LN2 comes out of the other vent hole.
Then proceed to the experiment as you would when working under ambient temperature. Use the external DC power supply and the PI Temperature Controller SIM
to heat up the base plate, and the Pulse Current SIM to heat up the addendum as before. Then, repeat the experiment with the empty addendum, and subtract the \(C\) for the empty addendum
from the \(C\) value for the addendum with tin as before. You will be recording the values at 85, 95, 105, 115, 125, 135 K. Please refer to previous experiment,
if you are unsure what to do.
You cannot power down the vacuum while there is still LN2 in the reservior, since moisture from the air would freeze to everything inside. To power down vacuuming after LN2 run (after experiment completion or when taking the tin sample out to do the empty addendum run), wait until everything inside warm up to about room temperature, possibly over the day/night, before powering down the vacuum, and opening up the dewar as usual.
The process to this is the same as you would do in Experiment 1 Data Analysis. Use the same mV to Kelvin conversion values in the table as before.
From Experiment 1 and 2, you should be able to see that the specific heat is not a constant quantity as suggested by the Dulong-Petit model. Rather, it is not constant, and looks more like the Einstein model. However, the Debye model is in even better agreement with the results than the Einstein model, and you will be learning/proving this in Experiment 3.
The Einstein's model although qualitatively reproduces the temperature dependance of specific heat, it is not entirely accurate. This is because the
Einstein's model assumes that all simple harmonic oscillator oscillates at one frequency \(\omega\) but this is simply not true. This is where Debye's model
comes in. The Debye's model assumes that there are whole range of allowed frequencies and assigns one frequency to each classical 'normal mode of
vibration' in an elastic solid. The lowest frequency is the one where half its wavelength spans the whole size of the solid body. The normal mode of
vibration is allowed to follow a statistical law with density of the frequency state approaching \(\omega^2\) (as is expected for a three-dimensional object).
The highest allowed frequency results from the total number of allowed modes and cutting off the range of allowed modes once \(3N\) vibrational
modes have been assigned (\(N\) is the number of harmonic oscillators). A quantum-mechanical model is used when assigning energy to these vibrational modes.
The resulting model takes the form below:
$$c_V\space(1\space mole)=9R\left(\frac{T}{T_D}\right)^3\int_0^{T_D/T}\frac{y^4e^y}{\left(e^y-1\right)^2}dy$$
where \(T_D\) is the Debye's Temperature, which is an intrinsic property of each substance.
The
full derivation of the Debye's model is available here, for those who are curious.
In this experiment, you will get to find the specific heat and then fit the data to both Einstein's and Debye's model and qualitatively compare (especially at low temperature), which model gives a better result.
Tin was picked as the sample for Experiment 1 and 2 due to its ability to give a very different results at LN2 and ambient temperature. However, tin does not show strong deviation between Einstein and Debye's model, even at low temperature, so alumina (Al2O3) is chosen instead for this experiment for that purpose.
In this experiment, firstly record the mass of the alumina sample before putting it on the adendum. Now, record the heat capacity \(C\) at room temperature at approximately the same temperature steps as you did in Experiment 1. You do not need to do the empty addendum run since you have already done that previously in Experiment 1. Use the empty addendum data and the same method as in Experiment 1 to subtract the \(C\) of the empty addendum from the \(C\) of the addendum-with-sample data. Then, run the same experimeent at LN2 temperature taking the data at approximately the same temperature steps as you did in Experiment 2. Again, you do not need to do the empty addendum run, since you have already done so in Experiment 2. Again, subtract the \(C\) of the empty addendum from the \(C\) of the addendum-with-sample data like you did in Experiment 2. Then, divide out the mass of the alumina sample you measured earlier — this should give you the specific heat \(c_V\) of alumina as a function of temperature over the range from LN2 temperature to ambient temperature with the unit of J/g/K. However, I would like you to convert these \(c_V\) values to the unit of J/mol/K (Hint: The literature value for the molar mass of alumina is 101.961 g/mol). Now, plot these \(c_V\) values on the graph, then fit these \(c_V\) values to the two model: the Einstein's model and the Debye's model. As a reminder, the Debye's model function and the Einstein's model function is given again below:
| Einstein | $$c_V\space(1\space mole)=3R\left(\frac{T_E}{T}\right)^2\frac {e^{T_E/T}}{\left(e^{T_E/T}-1\right)^2}$$ |
| Debye | $$c_V\space(1\space mole)=9R\left(\frac{T}{T_D}\right)^3\int_0^{T_D/T}\frac{y^4e^y}{\left(e^y-1\right)^2}dy$$ |
If you did not know how to enter an integral before this lab, here is how to do it. Let's say you want to calculate the following integral: $$\int_0^5 2x^2+3x+4 \space dx$$ You will use the following code to calculate this.
import scipy.integrate as integrate
result = integrate.quad(lambda x: 2*x**2+3*x+4, 0, 5)
result
(140.83333333333337, 1.5635640930137626e-12) The first result in this tuple is the result of the
integration and the second result is an estimate of the absolute error in the result. You can do the following, if you want to get
rid of the absolute error output.
import scipy.integrate as integrate
result, err = integrate.quad(lambda x: 2*x**2+3*x+4, 0, 5)
result
err,
separately from the result variable.
If you want to say infinity or negative infinity in these integral calculation, use
numpy.inf and -numpy.inf, respectively.
More information on scipy.integrate can be found here.
From here, you should be able to see that the Debye's model qualitatively fits better than the Einstein's model! Now, to see how close your result is to the literature result, plot also, the graph of Debye's model function but this time, the literature value of the Debye's temperature \(T_D\) of Alumina is given as 980 K.